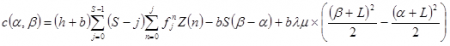راهاندازی سیستم کنترل موجودی با شروع تقاضا در زمان معین
موضوع: آموزش حسابداری
فرض استاندارد در مدلهای موجودی احتمالاتی این است که به حالت پایدار رسیدهایم. بنابراین سیاست بهینه تنها مستقیماً تحت این فرض کاربرد دارد. اما هنگامی که فروش قلم جدیدی را شروع میکنیم معمولاً مشکل راهاندازی نیز پیش میآید. ممکن است شرکت رسماً اعلام کند که در تاریخی معین فروش قلم جدیدی را شروع میکند. بنابراین هیچ تقاضایی پیش از آن تاریخ وجود ندارد.
در این مقاله چنین وضعیتی را بررسی میکنیم. تقاضای احتمالاتی به شکل فرآیند مرکب پواسون در زمانی خاص به نام زمان صفر شروع میشود. غیر از این تمامی فرضها استاندارد هستند. هزینههای نگهداری و پسافت برای واحد و زمان واحد وجود دارد. هیچ هزینه راهاندازی یا سفارش وجود ندارد از این رو هیچ منفعتی برای سفارش دادن در دستهها وجود ندارد. مدت زمان تحویل برای تجدید موجودی ثابت است.
قبل از این مسائل راهاندازی مرتبط در خصوص کنترل موجودی در چند مقاله بررسی شده است. یکی از وضعیتها در که در چند مقاله بررسی شده است هنگامی پیش میآید که تقاضا تا زمان تحویل دسته نتواند برآورده شود، هیچ ذخیره اولیهای وجود نداشته و نرخ تولید محدود باشد. بنابراین بهینه آن است که از کمیتهای کوچکتر دسته اولیه استفاده شود تا بتوان تقاضا را زودتر برآورده کرد. مدلهایی که به این جنبه میپردازند از جمله عبارتند از آکساتر (1988)، دینگ و گروبستروم (1991) و گروبستروم و دینگ (1993). آکساتر (در دست چاپ) وضعیت مرتبطی را بررسی کرده است که در آن پیشبینیها در حال بهبود هستند. او در مقالهاش ثابت میکند که این امر نیز بر کمیتهای دسته اولیه تأثیر میگذارد. تاثیرات یادگیری و فراموشی نیز از دلایل دیگر استفاده از کمیتهای دسته اولیه هستند که سبب تغییر نرخ تولید میشوند. برای مثال به المغربی (1990) و کلاستورین و معینزاده (1989) مراجعه کنید.
این مقاله به صورت زیر تنظیم شده است. بخش 2 به توصیف مشروح مسئله مورد نظر میپردازد. سیاست بهینه در بخش 3 تعیین میشود. در نهایت چند نتیجهگیری در بخش 4 ارائه میگردد.
2 فرمولبندی مسئله
در این مقاله وضعیتی را بررسی میکنیم که در آن یک انبار با تقاضای گسسته مرکب پواسون مشتری مواجه است. تقاضاهایی که مستقیماً برآورده نشوند پسافت میشوند. هزینههای استاندارد نگهداری و پسافت را در نظر میگیریم. هیچ هزینه سفارشدهی وجود ندارد. مدت زمان تحویل برای تجدید موجودی ثابت است. همچنین وضعیت مرور را دائم فرض میکنیم.
در فرضیات مورد بررسی به خوبی معلوم میشود که سیاست کنترل بهینه در حالت پایدار، سیاست (S-1, S) یا به صورت معادل سیاست S است یعنی هنگامی که موقعیت موجودی (انبار در دست کار، به اضافه سفارشهای معوقه و منهای پسافتها) به زیر سطح بهینه سطح سفارش تای S کاهش یابد. سفارش به گونهای راهاندازی میشود که موقعیت موجودی را به S برگرداند. این سیاستها در عمل متداول هستند. این امر بهویژه برای قطعات یدکی نسبتاً گران با تقاضای پایین برقرار است.
البته سیستم را در حالت پایدار در نظر نمیگیریم. طبق فرض، فرآیند تقاضا در زمان صفر شروع میشود. پیش از این زمان هیچ تقاضایی وجود ندارد. البته میتوانیم در هر زمانی پیش یا پس از زمان صفر اقدام به سفارش کنیم و مدت زمان تحویل برای تجدید موجودی ثابت و برای تمامی سفارشها یکسان است.
ابتدا نشانههای پایه زیر را معرفی میکنیم:
L مدت زمان تحویل برای تجدید موجودی
S موقعیت موجودی سفارش تا
D(t) تقاضای احتمالاتی طی زمان t
λ شدت رسید مشتری
fj احتمال برای کمیت تقاضا j، 0= fj برای 1 >j
fjn احتمال برای تعداد کل واحدهای تقاضا شده توسط n مشتری برابر j است یعنی کانولوشن nتایی fj
µ =میانگین اندازه تقاضای مشتری،
h هزینه نگهداری غیرمنفی برای هر واحد در هر زمان واحد
b هزینه پسافت غیرمنفی برای هر واحد در هر زمان واحد
IP موقعیت موجودی
IL سطح موجودی
توزیع پواسون تجمعی
3 سیاست بهینه
3-1 سیاست بهینه حالت پایدار
ابتدا وضعیت حالت پایدار را در نظر بگیرید. هنگام اعمال سیاست (S-1, S) چگونگی تعیین هزینههای مورد انتظار به خوبی معلوم است (برای مثال برای توضیحات بیشتر به آکساتر، 2006 مراجعه کنید). زمان اختیاری t و نیز زمان t+L را در نظر بگیرید. سفارشهایی که در بازه [t+L ، t) راهاندازی شده باشند به خاطر مدت زمان تحویل در زمان t+L به موجودی انبار نمیرسند اما هر چیزی که پیشتر در زمان t سفارش داده شده به موجودی انبار رسیده است. در نتیجه داریم:
(1)
که در آن D(t, t+L) یا به صورت سادهتر D(L) تقاضای مدت زمان تحویل احتمالاتی است.
فرض کنید که موقعیت انبار در تمامی اوقات برابر S نگهداشته شود و هزینههای متناظر مورد انتظار نگهداری و پسافت برای واحد زمان برابر C(S, L) باشد. با استفاده از (1) داریم:
(2)
که در آن از علامتگذاری زیر استفاده میکنیم: و . توجه کنید که . در (2) n برابر تعداد مشتریان طی مدت زمان تحویل است که دارای توزیع پواسون میباشد. همچنین j تقاضای متناظر میباشد. یادآوری میشود که احتمال این امر است که n مشتری تقاضای کلی j را حاصل کنند. سطح موجودی در زمان t+L برابر S-j است.
C(S, L) در S محدب است و S=0 کران پایینتر سطح سفارش تا میباشد. (S کمتر هزینههای پسافت بالاتری حاصل میکند اما هزینههای نگهداری را کاهش نمیدهد.) بنابراین با شروع از کران پایینتر S=0 مقدار S را بهینه میکنیم و آنگاه مقدار S را هر بار به میزان یک واحد افزایش میدهیم تا آنکه بهینه محلی را بیابیم که بهینه کلی نیز هست. سیاست بهینه را با و هزینه بهینه متناظر را با نشان میدهیم. همچنین معلوم است که در L غیر نزولی است. (برای مثال این مطلب از (5-61) در آکساتر (2006) ص 103 نتیجه میشود).
3-2-سیاست راهاندازی رسمی
اکنون به موردی میپردازیم که در آن تقاضا در زمان صفر شروع میشود. بدیهی است که پیش از زمان صفر خواهان هیچ تحویلیای نیستیم. این امر به معنای آن است که پیش از زمان –L نباید هیچ سفارشی داشته باشیم. با سفارش در زمان t-L میتوانیم تحویلیها را در هر زمان t≥0 به دست آوریم. حال قضیه ساده زیر را بیان میکنیم.
قضیه 1: اعمال سیاست از زمان صفر اقدامی بهینه است.
برای اینکه ببینیم گزاره 1 درست است فقط کافی است توجه کنیم که (1) و (2) برای t≥0 معتبر هستند و این که سیاست بهینه را به همان شیوهای به دست میآوریم که سیاست حالت پایدار بهینه را در بخش 3-1 به دست آوردیم.
در مرحله بعدی این سیاست را در بازه باقیمانده در نظر می گیریم و داریم
قضیه 2: در بازه اعمال سیاست متغیر زمانی اقدامی بهینه است. در زمان t سطح بهینه سفارش تا برابر است با . (توجه کنید که هنگامی که t از –L به صفر افزایش مییابد، طول بازه مورد نظر t+L از صفر به L افزایش مییابد.)
اثبات: سیاست سفارشدهی را در در نظر بگیرید و IPt را برابر سفارشهای تجمعی در زمان t در نظر بگیرید یعنی سفارشهای واقع در بازه .
توجه کنید که IPt باید غیرنزولی باشد. یادآوری میشود که هیچ تقاضایی در وجود ندارد. همه چیزی که در IPt گنجانده میشود در زمان t+L به موجودی انبار میرسد اما سفارشهای دیرتر این گونه نیستند. در نتیجه سطح موجودی در زمان t+L را به صورت زیر به دست میآوریم:
(3)
با توجه چگونگی به دست آوردن سیاست بهینه در حالت پایدار در بخش 3-1 بدیهی است که اگر باشد هزینههای مورد انتظار در t+L را به حداقل میرسانیم. این هم سیاست بهینهای است زیرا غیرنزولی است بنابراین با اعمال سطح سفارش تای از این موقعیت موجودی انبار برای تمامی تبعیت کنیم. از این رو قضیه ثابت میشود.
3-3 تعیین عددی قاعده تصمیمگیری
برای اعمال سیاست بهینه لازم است را برای مقادیر مختلف t تعیین کنیم. برای داریم زیرا نرخ هزینه در زمان صفر برابر صفر است. فقط پیش از داریم . با افزایش t از –L به صفر نیز به صورت گام به گام و هر بار یک واحد از به افزایش خواهد یافت.
بدیهی است که هنگامی که باشد تعویض از S به S+1 باید رخ دهد. توجه کنید که این تعویض باید هر بار یک واحد باشد. برای اثبات این مطلب فرض میکنیم که تعویض از S به S+k صورت میگیرد و این که k>1. سپس باید فرض کنیم که و هم S و هم S+k بهینه هستند. اما به علت محدب بودن، به مقادیر میانی مانند S+1 هزینههای کمتری هم داده میشود که این تناقض است.
با جستجوی دوبخشی به آسانی میتوان نقاط تعویض بهینه را تعیین کرد. فرض کنید که tk زمانی است که تعویض به سطح سفارش تای k بهینه باشد. یادآوری میشود که بزرگترین مقدار kایی که برای بررسی نیاز داریم برابر است. فرض کنید که tk-1 نامعلوم باشد. (یادآوری میشود که ). بدیهی است که tk-1 حد پایینی tk است یعنی . برای حد بالایی میتوانیم از استفاده کنیم. میتوانیم مقدار جدیدی از زمان تعویض را به صورت به دست آوریم. روشن است که اگر میدانیم که t میتواند به عنوان کران پایینتر بهبود یافته و در غیراینصورت به عنوان کران بالاتر بهبود یافته عمل کند. این کار را تا جایی ادامه میدهیم که فاصله بین کرانها به اندازه کافی کوچک شود.
3-4 مثال
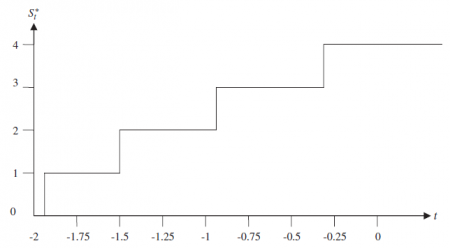
برای توضیح تعیین سیاست بهینه، تقاضای خالص پواسون یعنی را در نظر میگیریم. همچنین شدت رسیدهای مشتری است. مدت زمان تحویل در واحد و زمان واحد است و هزینه پسافت در واحد و زمان واحد است. با استفاده از (2) سطح سفارش تای حالت پایدار بهینه را به صورت تعیین میکنیم. سپس نقاط تعویض را از صفر به 1/1 به 2/2 به 3 و از 3 به 4 تعیین میکنیم به ترتیب زمانهای 905/1-، 498/1-، 944/0- و 315/0- را به دست میآوریم. سیاست سفارش تا در شکل 1 نشان داده شده است.
3-5 ارزیابی هزینه
میدانیم موقعیت موجودی بهینه سفارش تا به صورت تکهای ثابت است و هر بار در بازه یک واحد افزایش مییابد. سیاست در این بازه هزینههای ناپایدار را در بازه تعیین خواهد کرد. هزینههای مورد انتظار را باید در این بازه تعیین کنیم. بعد از این بازه هزینههای بهینه حالت پایدار را داریم که لازم نیست مجدداً بررسی کنیم. پس توجه خود را به هزینههای بازه محدود میکنیم. فرض میکنیم موقعیت موجودی بهینه در بازه برابر S باشد که در آن . هزینههای مورد انتظار متناظر در بازه به صورت نوشته میشوند. زمان t را در بازه مورد نظر در نظر بگیرید. تقاضای مدت زمان تحویل متناظر در زمان t+L برابر تقاضای پواسون مرکب است. یادآوری میکنیم که تقاضا در زمان صفر شروع میشود.
شکل 1-مثالی از سیاست بهینه. تقاضای پواسون،
با استفاده از (2) به دست میآوریم:
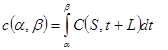
(4)
حال تعریف میکنیم
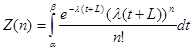
(5)
توجه کنید که احتمال آن است که متغیر با توزیع احتمالاتی ارلانگ با n+1 مرحله، مقداری بین و را خواهد گرفت. این امر به معنای آن است که که میتوانیم را به صورت زیر تعیین کنیم
(6)
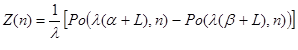
و
(7)
با استفاده از میتوانیم به آسانی هزینهها را برای هر زیربازه با سطح سفارش تای ثابت خاص S تعیین کرده و سپس نهایتاً هزینهها را برای این بازهها جمع ببندیم. توجه کنید که این زیربازهها دارای S برابر با 0، 1، 2، ...، هستند یعنی به تعداد از این زیربازهها وجود دارد.
جدول 1-نتایج عددی. تقاضای پواسون. پارامترهای ثابت: و .
|
مدت زمان تحویل L |
هزینه پسافت b |
بهینه |
افزایش هزینه خطی، % |
% افزایش هزینه |
% افزایش هزینه |
|
1 |
1 |
0.46 |
4.4 |
9.3 |
67.1 |
|
1 |
5 |
1.13 |
5.2 |
122.0 |
48.4 |
|
1 |
10 |
1.45 |
21.4 |
245.8 |
25.4 |
|
1 |
15 |
1.65 |
17.6 |
354.6 |
56.5 |
|
2 |
1 |
1.39 |
2.8 |
43.7 |
90.2 |
|
2 |
5 |
3.12 |
10.0 |
220.6 |
48.5 |
|
2 |
10 |
3.96 |
15.4 |
405.4 |
60.0 |
|
2 |
15 |
4.44 |
29.2 |
576.3 |
46.1 |
|
4 |
1 |
4.09 |
1.8 |
95.6 |
131.9 |
|
4 |
5 |
8.68 |
7.3 |
361.0 |
93.9 |
|
4 |
10 |
10.83 |
14.4 |
638.7 |
89.9 |
|
4 |
15 |
12.07 |
26.7 |
894.4 |
72.6 |
|
8 |
1 |
11.80 |
1.1 |
171.3 |
198.9 |
|
8 |
5 |
24.11 |
6.7 |
563.6 |
138.5 |
|
8 |
10 |
29.78 |
14.9 |
974.7 |
119.5 |
|
8 |
15 |
33.03 |
19.3 |
1353.1 |
120.7 |
3-6 مقایسه با راه حل ابتکاری ساده
تاکنون چگونگی به دست آوردن سیاست بهینه و هزینههای متناظر را نشان دادهایم. کار محاسباتی آن بسیار محدود است. با اینحال شاید جالب باشد راه حل بهینه را با راهحل ابتکاری سادهتر مقایسه کنیم. راه حل بهینه، بازه را به زیربازههای تقسیم میکند که در آن میتوانیم از در زیربازه اول، در زیربازه دوم، ... و نهایتاً در زیربازه آخر استفاده کنیم. هنگام به دست آوردن راهحل بهینه، طول زیربازهها را بهینهسازی میکنیم. در مثال بخش 3-4، نقاط تعویض به صورت 905/1، 498/1-، 944/0- و 315/0- به دست آمدند (این مثال نیز مسئله هفتم در جدول 1 زیر است). در جدول 1 راهحل ابتکاری سادهای را ارزیابی کردهایم که در آن زیربازههای مورد بررسی دارای طول یکسانی هستند. این امر به معنای آن است که نقاط تعویض به صورت خطی افزایش مییابند. در جدول 1، این راهحل را عنوان راهحل «خطی» مینامیم. برای مثال در بخش 3-4، نقاط تعویض به صورت 6/1-، 2/1-، 8/0- و 4/0- به دست میآیند. در جدول 1 16 مسئله را با تقاضای پواسون در نظر میگیریم که همگی آنها دارای و هستند. تمامی ترکیبات و گنجانده میشوند. هنگام استفاده از راهحل ابتکاری داده شده در ستونهای 3 و 4، هزینههای بهینه و هزینه نسبی افزایش مییابند. افزایش هزینه میانگین 4/12% و بیشینه افزایش 2/29% است. این نتایج نشان میدهند که در حالت کلی رسیدن به راهحل بهینه ارزش صرف زمان محاسباتی بیشتر را دارد.
در جدول 1، هزینههای دو راهحل ساده دیگر را نیز ارزیابی کردهایم. یک راهحل به معنای آن است که در بازه داریم یعنی هیچ پیش از زمان L هیچ چیزی در انبار نباشد و تقاضای مشتری با تاخیر L برآورده شود. همانگونه که انتظار میرود، این راهحل به ویژه برای مدتزمانهای تحویل طولانی و هزینههای پسافت بالا راهحل بسیار بدی است. در راهحل دیگر، در زمان –L از راهحل حالت پایدار استفاده میکنیم. این راهحل بهتر است اما هزینههای اضافی به ویژه برای مدتزمانهای تحویل طولانی همچنان بسیار بالاست.
4نتیجهگیری
در این مقاله مسئله کنترل موجودی ناپایدار بررسی گردیده است. فرآیند تقاضای احتمالاتی در زمان معین خاص شروع میشود. صرفنظر از این، تمامی فرضیهها استاندارد هستند. مدت زمان برای تجدید موجودی معلوم است. هزینههای مورد بررسی عبارتند از هزینههای نگهداری و پسافت اما هیچ هزینه راهاندازی یا سفارشدهی وجود ندارد. نسبتاً بدیهی است که سطح سفارش تا پیش از شروع تقاضا باید کمتر باشد. در این مقاله اثبات کردهایم که سیاست سفارش بهینه سیاست سفارش تای متغیر زمانی است که تعیین آن آسان است.
مراجع
Axsater, S., 1988. Initial order quantities. Engineering Costs and Production Economics 15, 307-310.
Axsater, S., 2006. Inventory Control, 2nd ed. Springer, New York.
Axsater, S. Batch quantities when forecasts are improving. International Journal of Production Economics (in press).
Ding, H., Grubbstrom, R.W., 1991. On the optimization of initial order quantities. International Journal of Production Economics 23, 79-88.
Elmaghraby, S.E., 1990. Economic manufacturing quantities under conditions of learning and forgetting (EMQ/LaF). Production Planning & Control 1, 196-208.
Grubbstrom, R.W., Ding, H., 1993. Initial Order Quantities in a Multistage Production System with Backlogging. International Journal of Production Economics 30-31, 153-166.
Klastorin, T.D., Moinzadeh, K., 1989. Production lot-sizing under learning effects: an efficient solution technique. IIE Transactions 21, 2-8.
به این مطلب چه امتیازی میدهید؟
4از 5 امتیاز
نظرات